No products in the cart.
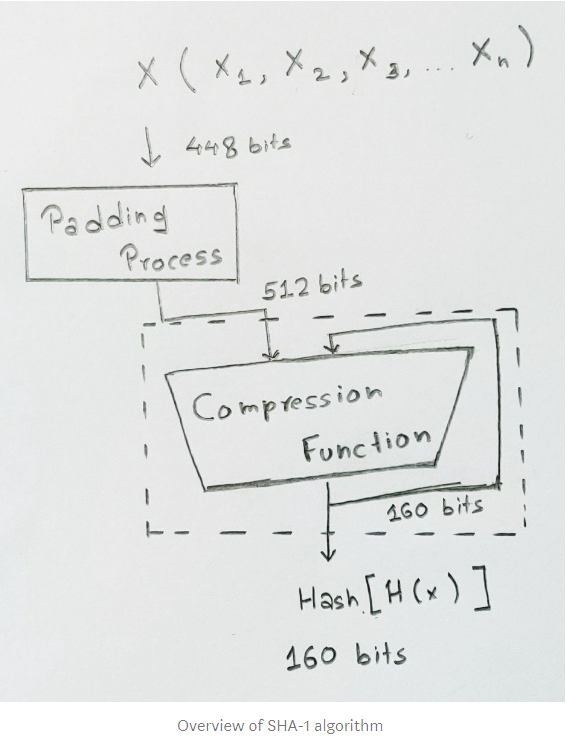
Breaking Down: SHA-1 Algorithm by Aditya Anand I haven’t been blogging for the past month or so and to be true the reason for that was that I totally out of content. You could say I simply ran out of gas, so I took this time off and went back....
Author
Latest Articles
BlogDecember 28, 2022Cybersecurity in Education: What Parents, Teachers, and Students Should Know in 2023
BlogDecember 15, 2022Remembering Leonard Jacobs
BlogSeptember 30, 2022VPN Security: A Pentester's Guide to VPN Vulnerabilities
BlogAugust 9, 2022AppSec Tales II | Sign-in
Hi, great post.
can you get the sha1 at the same time you compress the file? Meaning if I compress any file can I find the sha1 without going through all the sha1 again?
Doesn’t the pigeonhole problem (collisions) nullify your second rule that no two messages have the same digest?